主席树

发表于 |

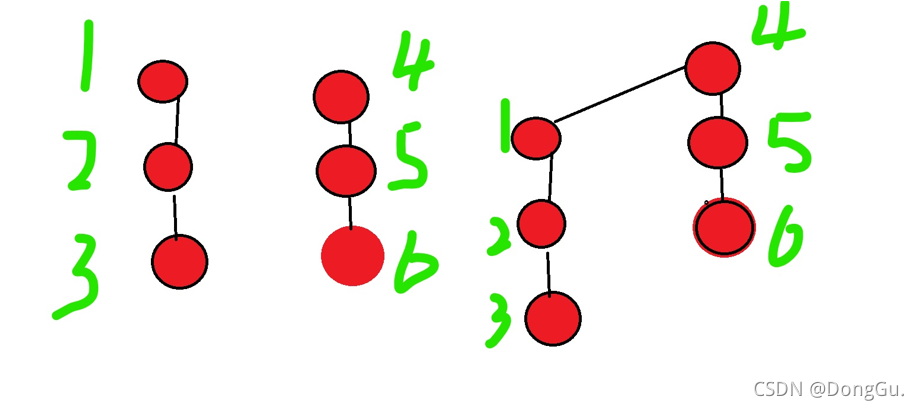
直接上个图

ps（题目）

1
2
3
4
5
6
7
8
依照这个数据 画的图
5 5
25957 6405 15770 26287 26465 
2 2 1
3 4 1
4 5 1
1 2 2
4 4 1

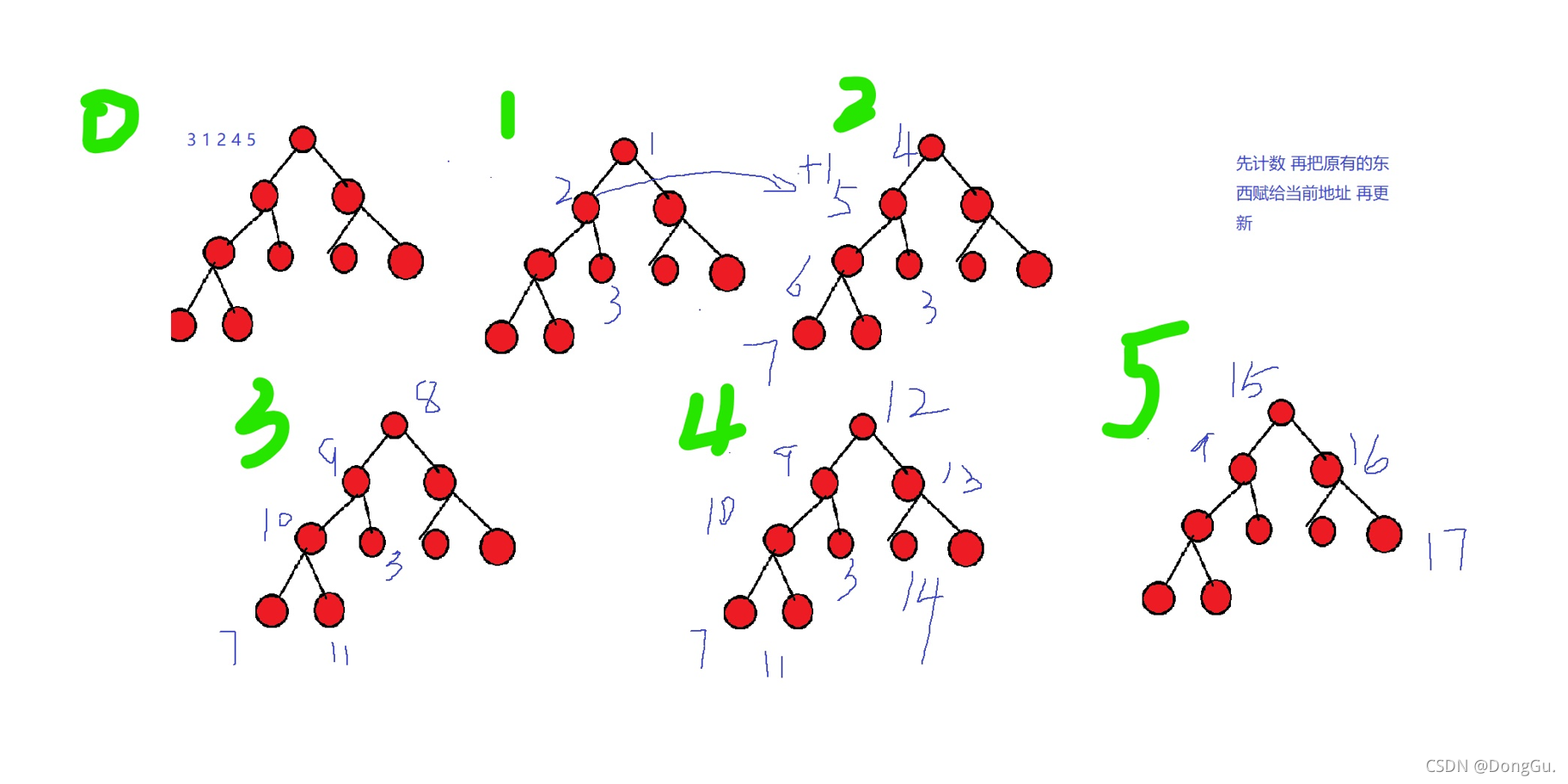
1. 什么是可持久化

就是说 你要去访问之前的状态， 感觉有点像dp和哈希， 每个点的标号来决定一个状态

2. 主席树它能带来什么效果

就我自己感觉来说，就是两颗一模一样的树，不是完完全全复制，而是有选择的复制，从图也可以看出，好好看这张图的编号，它可以节省空间，节省时间，hjt大佬Orz

3. 我一开始最难接受的部分……

  • 就是动态开点，引用& 的使用，但是如果在建造的时候不用引用，你会发现根本就改不了实际值，然后还得加上好多好多行代码来实现，没必要，
  • 引用&：就是为了递归中更好修改每个节点的左右子树，对， 就这样， 接受它的存在

洛谷主席树

模板题

  • 因为它的数值范围太大，需要离散化，这里用的是stl的unique
  • 然后类似前缀和的思想，k < sumL , 就往左子树去，相反，就去右子树
  • 再看看图
  • 最后查询的时候不要去按原数值输出，因为它建立的时候是类似权值线段树，输出应该是离散化后的数值下标
  • root[] : 每个i 都给它建立一颗树，但不需要每个点都建，而是有选择的开点 存数据，看图，类似i == 3 时 10号点的左子树是7 是i == 2 的版本，而它要存的是右子树，然后开点存11节点的数据，那么root[i], 就是每个版本的根节点的数值，这样能更好的管理；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

const int maxn = 2e5 + 5;
int a[maxn];
vector<int> v;
inline int getid(int x) { return lower_bound(v.begin(), v.end(), x) - v.begin() + 1; }

struct Node{
    int l, r, sum;
}hjt[maxn * 40];

int cnt, root[maxn];

void insert(int l, int r, int pre, int& now, int p){
    hjt[++cnt] = hjt[pre];
    now = cnt;
    hjt[now].sum++;
    if (l == r) return;
    int m = (l + r) >> 1;      
    if (p <= m) insert(l, m, hjt[pre].l, hjt[now].l, p);
    else		insert(m + 1, r, hjt[pre].r, hjt[now].r, p);
}

int query(int l, int r, int L, int R, int k){
    if (l == r) return l;
    int m = (l + r) >> 1;
    int tmp = hjt[hjt[R].l].sum - hjt[hjt[L].l].sum;
    if (k <= tmp) return query(l, m, hjt[L].l, hjt[R].l, k);
    else 		  return query(m + 1, r, hjt[L].r, hjt[R].r, k - tmp);
}

signed main(){
    #ifdef HZD
        freopen("in.in", "r", stdin);
        freopen("out.out", "w", stdout);
    #endif

	int n, m; cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        v.push_back(a[i]);
    }
    sort(v.begin(), v.end());
    v.erase(unique(v.begin(), v.end()), v.end());

    for (int i = 1; i <= n; i++) {
        insert(1, n, root[i - 1], root[i], getid(a[i]));
    }

    while (m--) {
        int l, r, k; cin >> l >> r >> k;
        // 是v 而不是 a
        cout << (v[query(1, n, root[l - 1], root[r], k) - 1]) << "\n";
    }
    return 0;
}

可持久化数组

（模板题）

在这里插入图片描述

  • 既然说道每个操作对应一个版本，那我们可以想到上一道题，主席树的root，就是来存每个根节点的值，
  • 那这里我们直接更新root所对应树进行修改就ok了
  • 询问的话 就把你要的第几个版本的树丢到query函数去
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <iostream>
#include <algorithm>
using namespace std;

#define lson l, mid
#define rson mid + 1, r

typedef long long ll;
const int N = 1e6 + 10;

int cnt;
int a[N];
int root[N];
struct Node{
	int l, r, val;
}hjt[N * 40];

void build(int l, int r, int &now)
{
	now = ++cnt;
	if (l == r) {
		scanf("%d", &hjt[now].val);
		return;
	}
	int mid = l + r >> 1;
	build(lson, hjt[now].l);
	build(rson, hjt[now].r);
}

void updata(int l, int r, int pre, int &now, int pos, int val)
{
	now = ++cnt;
	hjt[now] = hjt[pre];
	if (l == r && l == pos) {
		hjt[now].val = val;
		return;
	}

	int mid = l + r >> 1;
	if (pos <= mid) updata(lson, hjt[pre].l, hjt[now].l, pos, val);
	else            updata(rson, hjt[pre].r, hjt[now].r, pos, val);
}

int query(int l, int r, int now, int pos)
{
	if (l == r) return hjt[now].val;

	int mid = l + r >> 1; 
	if (pos <= mid) return query(lson, hjt[now].l, pos);
	else			return query(rson, hjt[now].r, pos);
}

signed main()
{
#ifdef HZD
	freopen("in.in", "r", stdin);
	freopen("out.out", "w", stdout);
#endif

	int n, q; scanf("%d%d", &n, &q);
	build(1, n, root[0]);

	for (int i = 1; i <= q; i++)
	{
		int pre, op, pos, val; scanf("%d%d%d", &pre, &op, &pos);

		if (op == 1) {
			scanf("%d", &val);
			updata(1, n, root[pre], root[i], pos, val);
		}
		else {
			printf("%d\n", query(1, n, root[pre], pos));
			root[i] = root[pre];
		}
	}
	return 0;
}

可持久化并查集

(模板)

  • 其实思想还是和前面一样，在这里就分享一下怎么去更新父亲fa，高度deep
  • 我们都知道每个cnt开出来的点都有一个独一无二的标号，所以只要你传进来了一个根节点标号root[i], 你就可以知道每个叶子节点的fa 和deep，进而你就可以修改呀，查询呀，都是很基本的操作，和上面大同小异
  • 那么我感觉最难的就是这么去找父亲呢？如果还是用路径压缩，那还不是白忙活了，每次查找都要创造一个fa[i]数组，那会爆了，换一个用秩来结合，也就是高度矮的 移到 高的
    类似这样(合并1 4，发现两个高度相同，任取一个就行)在这里插入图片描述
    相应的， 当发现合并完之后，你要检查一下在此之前是不是两个集合的高度相同，是的话，还要去更新它的deep，像上图的4那样 deep[4] ++;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
#include <string>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;

typedef long long ll;
const int N = 2e5 + 10;

int cnt;
int n, m;
int root[N];

struct Node {
	int l, r, fa, deep;
}hjt[N * 40];

void build(int l, int r, int& now)
{
	now = ++cnt;
	if (l == r) {
		hjt[now].fa = l;
		return;
	}
	int mid = l + r >> 1;
	build(l, mid, hjt[now].l);
	build(mid + 1, r, hjt[now].r);
}

void updata(int l, int r, int pre, int& now, int pos, int val)
{
	now = ++cnt;

	hjt[now] = hjt[pre];

	if (l == r) {
		hjt[now].fa = val;
		return;
	}

	int mid = l + r >> 1;
	if (pos <= mid)	updata(l, mid, hjt[pre].l, hjt[now].l, pos, val);
	else			updata(mid + 1, r, hjt[pre].r, hjt[now].r, pos, val);
}

int query(int l, int r, int now, int pos)
{
	if (l == r) return now;
	int mid = l + r >> 1;
	if (pos <= mid)		return query(l, mid, hjt[now].l, pos);
	else				return query(mid + 1, r, hjt[now].r, pos);
}

void add(int l, int r, int pos, int now) 
{
	if (l == r)	{
		hjt[now].deep++;
		return;
	}
	int mid = l + r >> 1;
	if (pos <= mid) add(hjt[now].l, l, mid, pos);
	else            add(hjt[now].r, mid + 1, r, pos);
}

int find_fa(int ed, int x)
{
	int ff = query(1, n, ed, x);
	if (x == hjt[ff].fa) return ff;
	return find_fa(ed, hjt[ff].fa);
}

void solve()
{
	cin >> n >> m;
	build(1, n, root[0]);

	for (int i = 1; i <= m; i++)
	{
		int op, a, b; cin >> op;
		if (op == 1) {
			root[i] = root[i - 1];
			cin >> a >> b;
			int f1 = find_fa(root[i], a);
			int f2 = find_fa(root[i], b);

			if (hjt[f1].fa == hjt[f2].fa) continue;

			if (hjt[f1].deep > hjt[f2].deep) swap(f1, f2);
			updata(1, n, root[i - 1], root[i], hjt[f1].fa, hjt[f2].fa);  // 这里更新的只是修改fa 而没有改变deep
			if (hjt[f1].deep == hjt[f2].deep) add(root[i], 1, n, hjt[f2].fa); // 因为是把f1 接到f2 所以如果高度相等，那么f2这颗树就要+1
		}
		else if (op == 2) {
			cin >> a;
			root[i] = root[a];
		}
		else {
			root[i] = root[i - 1];
			cin >> a >> b;

			int f1 = find_fa(root[i], a);
			int f2 = find_fa(root[i], b);

			if (hjt[f1].fa == hjt[f2].fa) cout << "1\n";
			else cout << "0\n";
		}
	}
}

int main()
{
	int t = 1;
	while (t--) solve();
	return 0;
}
/*
10 10
1 4 1
2 1
1 9 3
3 5 8
2 3
1 6 2
1 5 7
2 4
3 1 9
2 6

*/

ps： 在这里还得感谢AgOH大佬的讲解，Orz

0%